Convolution Neural Network
수업 방향
CNN에 대해 배우기에 앞서 Convolution 계산 방식과 역전파 방식에 대해 알아보자.
수업 내용
Convolution 연산
- Convolution 연산은 kernel을 통해 연산이 되게 된다.
- kernel은 정해진 길이($k\times k$)로 정해져 있다.
- 이는 선형변환 중 하나로 param의 갯수를 줄이기 위한 방법 중 하나이다.
- 커널을 이용해 국소적으로 증가 또는 감소시킬 수 있다.
- 덧셈을 사용하기 때문에 원래는 cross-correlation이라 명해야 하지만 관용적으로 convolution 연산이라 명한다.
- 아래의 이미지는 convolution 연산의 진행 방식을 애니메이션화 한것이다.


- 위의 그림에서 노란색 부분이 연산 영역, 검은선이 실 결과이다.
N 차원에서의 Convolution 연산
- 차원이 늘어날 때 마다 kernel의 차원도 같이 늘어나게 되면 된다.
- 뭐가 어찌 되었건간에 kernel은 옮겨가며 크기가 고정되어야 한다.
- 수식으로 표현하면 다음과 같다.
$$ 1D: [f*g] (i)=\sum ^d _{p=1} f(p) g(i+p) $$
$$ 2D: [f*g](i, j)=\sum^d_{p=1}f(p,q)g(i+p, j+q) $$
$$ 3D: [f*g](i, j, k)=\sum^d_{p=1}f(p,q, r)g(i+p, j+q, k+r) $$
계산 예시
- 아래는 kernel 이다.
| 0 | 1 |
|---|---|
| 2 | 3 |
- 아래는 input 이다.
| 0 | 1 | 2 |
|---|---|---|
| 3 | 4 | 5 |
| 6 | 7 | 8 |
- 아래는 (1, 1)의 계산 결과다.
| 0 * 0 + 1 * 1 + 2 * 3 + 3 * 4 = 19 | 0 * 1 + 1 * 2 + 2 * 4 + 3 * 5 = 25 |
|---|---|
| … | … |
결과의 크기 결정
- 크기 $(H, W)$의 입력과 크기 $(H_K, W_K)$의 커널을 이용하여 계산하면 크기 $(O_H, O_W)$의 결과로 나오게 된다.
- 이를 계산하는 방법은 아래와 같다.
- $O_H=H-H_K+1$
- $O_W=W-W_K+1$
다채널에서 하나의 커널
- RGB 이미지와 같이 다중 채널로 오게 되는 경우 채널의 갯수 만큼 커널을 가지고 있어야 한다.
- kernel과 입력 각각을 convolution 계산을 하여 모두 다 더하여 하나의 output으로 출력한다.
- $(K_H,K_W,C)*(H,W,C)\rightarrow (O_H,O_W,1)$다
- 위의 수시과 같이 하나의 커널만 있기 때문에 결과가 하나의 레이어로 나온다.
- 단, 3개 이상의 채널인 경우 이때부턴 tensor 라고 명한다.
다채널에서 다중 커널
- 커널의 갯수가 다중인 경우 커널의 갯수만큼 출력이 나오게 된다.
Convolution 연산의 역전파
- 놀랍게도 back-propergation 과정에서도 convolution 연산을 사용한다.
- 먼저, forward 과정에서는 아래와 같다.
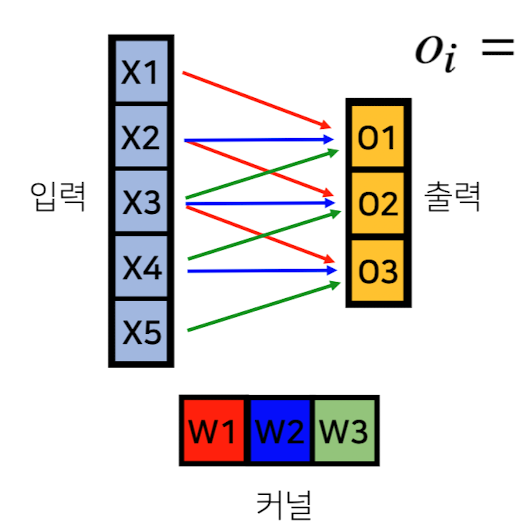
- back-propergation 할 때는 다음과 같다.
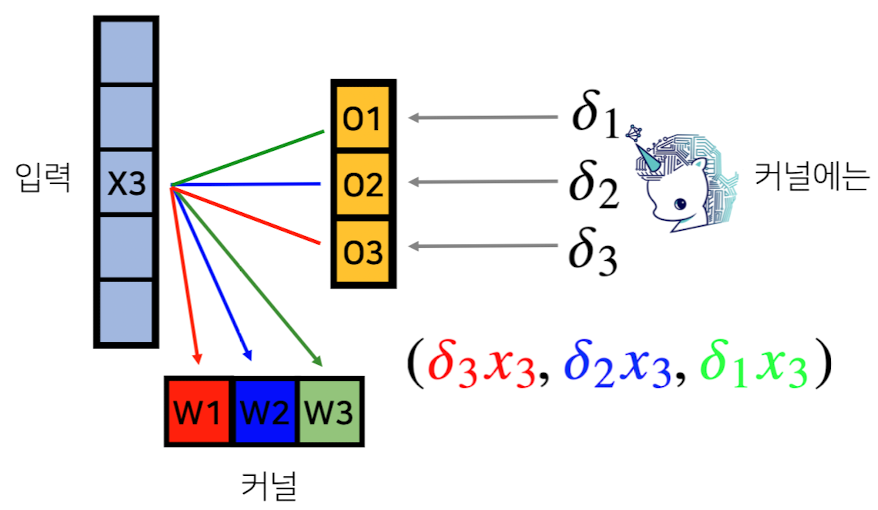
- Loss function에서 온 미분값($\delta_n$)과 입력값($x_n$)을 곱한 모든 값을 더하여 커널을 수정한다.
- $\frac{\partial L}{\partial w_1}=\delta_1x_1+\delta_2x_2+\delta_3x_3$ 쉽게 말해서, 미분 된 값을 kernel로 사용하고, 입력을 각각의 입력값을 주어 kernel에 값을 갱신한다.
- 이에 대해 back-propergation convolution을 통해 연산된 값을 각각 더하여 커널의 값을 갱신한다.